★扇形の中心角の求め方★途中式をていねいに解説!面積、弧の長さから求める方法 面積、弧の長さから求める方法 18–21 中学数学・理科の学習まとめサイト! まず、扇形の 「面積」 や 「弧の長さ」 を求める考え方ですが、「母線 x を半径とする円の面積 or 円周」 から 「おうぎ形の中心角の割合」 を掛けることで求めることができます。 母線 x と中心角 θ が分かっている場合、おうぎ形の弧の長さを求める式は次のようになります。 この式を利 \dfrac {x^2} {a^2}\dfrac {y^2} {b^2}=1 \ (a, b > 0) a2x2 b2y2 = 1(a,b > 0) で表される楕円の面積
扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com
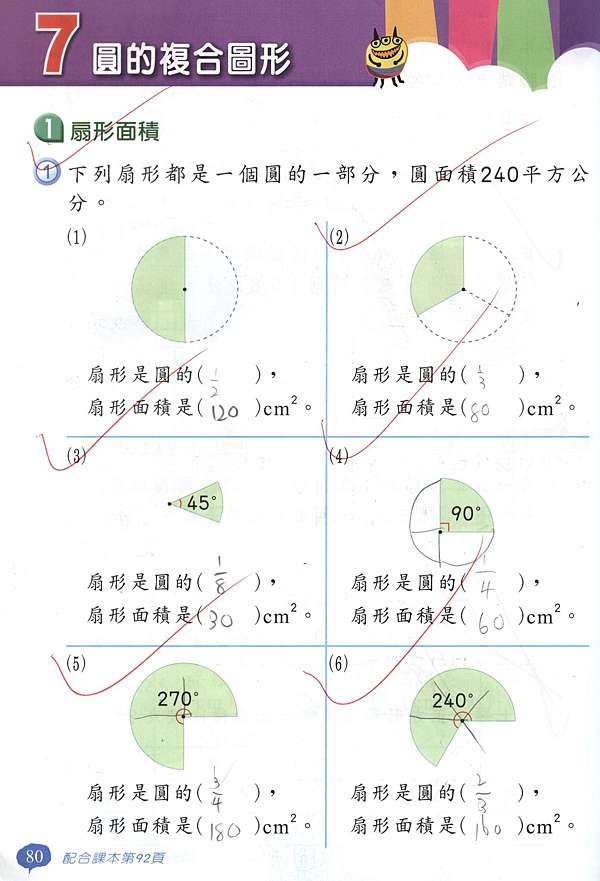
扇形の面積 求め方
扇形の面積 求め方- 問題 (正方形、長方形、平行四辺形、台形、ひし形、三角形、円を提示する) 面積の求め方が分かっている図形はどれでしょう。 四角形や三角形は求めることができます。 円はまだ学習していません。 これまでの面積の学習を生かして、円の面積の図形の面積の求め方(公式ほか) 正方形・円・長方形・平行四辺形・三角形・扇形・楕円・台形・双曲線・放物線・六角形・多角形 光正株式会社 役立つ資料シリーズ 図形の面積の求め方 A=面積 A=s 2 A=1/2d 2 S= d= d=1414 s=1414 A=面積 =弧の長さ a=角度 A=面積 A=面積 =弧の長さ




扇形の面積の求め方 公式と計算例
2 θ b a ( b − a) cos 2 θ) r ( θ) 2 = a 2 b 2 b 2 cos 2 θ a 2 sin 2 θ ( 2) e l l i p t i c a l a r c h L = a E ( x ( θ 0) a, k) − a E ( x ( θ 1) a, k) x ( θ) = r ( θ) cos θ, k = 1 − ( b a) 2, a ≥ b, π 2 ≥ θ ≥ 0 E ( x, k) 2 n d i n c o m p l e t e e l l i p t i c i n t e g r a l 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ: l l楕円の面積 a: b: 面積: 楕円の面積 a: b: 面積: 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l
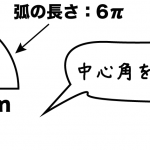
時間があったら、扇形の面積の求め方も復習してみてね^^ そんじゃねー Ken Ken Qikeruの編集・執筆をしています。 「教科書、もうちょっとおもしろくならないかな?」 そんな想いでサイトを始めました。 中1数学;どちらが正しいかわからないのでググったらL=314×半径×中心角/180という式の答えが 計算結果と同じになりました。 keisanより θの単位はラジアンになります。 単位を度にすると、ご指摘の通り L = 半径×π×中心角/180 となります。 2 1005 男 / 40歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 弧の長さ と 元の円の円周を 比較する このおうぎ形の元になった、 半径 3cm の円 を考えます 半径 3cm の円の 円周の長さ は $\textcolor{red}{直径(半径\times2)\times314}$ より $3\times2\times314=14 cm$ おうぎ型の弧の長さ(問題文より$314cm$)を比べると
扇形の面積の求め方 扇形の面積は、同じ半径の円の面積に 中心角の割合 をかければ求められます。 \begin{align}\text{(扇形の面積)} = \text{(円の面積)} \times \text{(中心角の割 《扇形の面積の求め方》 扇形の面積は、 円の面積に をかける ことで求められます。 この場合は =5024× =1256(㎠) 答え 1256㎠もう1本読んでみる 中1数学 意味から考える逆数の計算




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
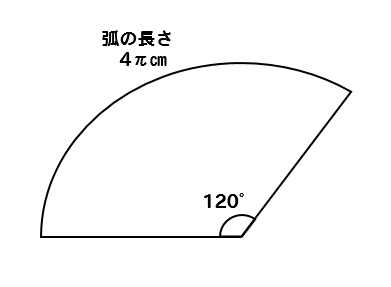
面積 おうぎ形の中心角の求め方と公式 中心角 問題 (1) 半径が 3cm、弧の長さが 3π cm のおうぎ形の中心角を求めなさい。 (2) 半径が 4cm、弧の長さが π cm のおうぎ形の中心角を求めなさい。 (3) 半径が 2cm、弧の長さが π/2 cm のおうぎ形の中心角を求めなさい。 (4) 半径が 3cm、弧の長さが 4π cm の扇形の面積 S × a ∘ 360 ∘ 例1) 中心角が 90 ∘ で、弧の長さが 628 c m の扇形の一辺の長さを求めなさい。 分からない部分を x として計算式にあてはめて計算します。 扇形の一辺の長さ x は直径の半分の長さですから、直径で計算する円周の式に 扇形の中心角をx°、弧の長さをL、半径をrとすると、 x = 180L/πr
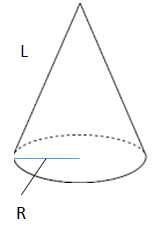



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題
扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。角度60°の扇形があります。半径が6です。面積を求めてください。 ★円錐の表面積★簡単な求め方とその理由を解説するぞ! kaztaro ゆい 円錐の表面積って めっちゃ難しいんですけどー かず先生 確かに難しい問題だね。 だけど、 簡単な求め方があるの知ってる? というわけで、今回の記事では円錐の表面積を簡単に求める方法について解説していく扇形の中心角を90°とする 扇形の面積は 扇形の弧の長さは 等しくなった 扇形の面積=弧の長さ×半径×1/2 これを「弧の長さ×半径×1/2」に代入すると これは扇形の面積を求める公式と同じ



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強
3分の1円の面積は,円の面積の3分の1だから 4分の1円の面積は,円の面積の4分の1だから 一般に中心角 の扇形の面積は,円の面積のx/360だから 中心角が分からない扇形の面積の求め方の裏ワザだよ。 ↓これ この扇形の弧の長さを15㎝、 AからCの長さは10cmにするよ。 この問題を普通にやると、 15 10x10xπx 10x2xπ =10x152 になるよ。 これでやるとめんどくさいし間違えやすくなるからここで裏ワザ! 10x15÷2って言うのは15㎝が底辺で10側面積(扇形の面積)は,π×× nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x° とおくと,扇形の弧の長さが底面の円周の長さと等しくなる



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
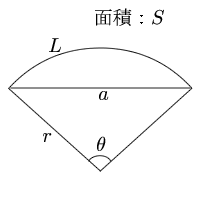
金属のブロックにひずみゲージを貼付して,荷重を負荷した時のひずみ測定結果と断面積と荷重より求めた応力(ひずみ値)との比較検証・・・応力σ = 荷重p ÷ 断面積aまず、半径「r」、中心角「θ」だけがわかっている弧の長さ「l」は ① また扇の面積「S」は ② まず①を変形して「πr=」の形にします。 ③ 同様にして②も変形して「πr=」の形にします。 ④ ③と④より 扇形の面積 =半径×半径×円周率× ※扇形の面積は、円の面積に をかけることで求めることが出来ます。 ※円周率は、小学校ではふつう314を使います。 扇(おうぎ)形の面積を求める公式3つと弧の長さの求め方をお伝えします。




扇形の面積の求め方 公式と計算例



扇形の面積
面積公式は、部分的に充填された円筒形の貯蔵タンクの体積を計算するのに用いることができる。 丸みのある天板を持つ窓やドアのデザインにおいて、 c と h だけが分かっているという場面で、製図士がコンパスで R を計算することに利用できる。・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。楕円 面積計算 公式 求め方 直径 半径 自動 長軸 短軸 面積 楕円 面積;




円の面積 練習応用 Youtube




扇形の面積の求め方 公式と計算例
扇形の弧の長さの求め方、弧度の意味など併せて勉強しましょう。 これが、円周を出す公式です。 扇型の中心角の求め方 いままでご紹介した扇形の公式を前提にして、問題において面積や弧の長さが与えられることによって、中心角を導くことを要求される問題があります。 円の面積の公式おうぎ形の面積の公式と求め方 教科書には扇形の面積や弧の長さを求める公式があります。 半径を\(\,r\,\),中心角 \(\,a^\circ\,\) として、 扇形の弧の長さ \(\,\ell\,\) と扇形の面積 \(\,S\,\) の公式は、 \(\color{red}{ \displaystyle \ell=2\pi r \times \frac{a}{360}\\ \displaystyle S=\pi r^2 \times \frac{a}{360}}\) となります
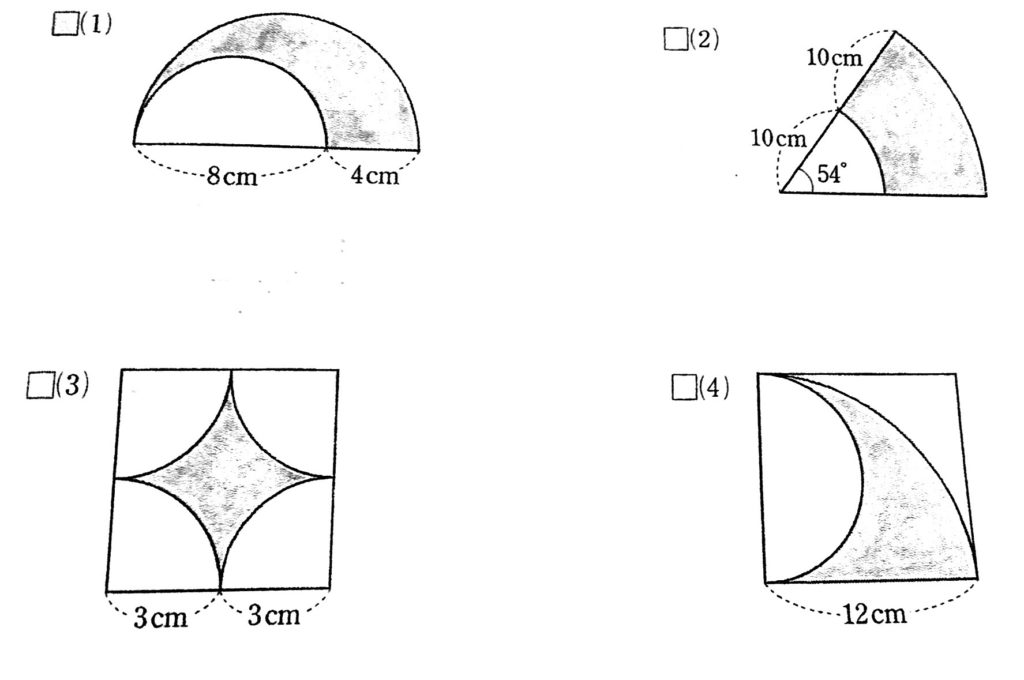



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




弓形の面積 香料ゐっすゐの夢




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか



おう ぎ 形 の 面積 求め 方




円弧面積の計算式



扇形の面積 小6です もう全くわかりません 問題はおうぎ形の中心 Yahoo 知恵袋




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
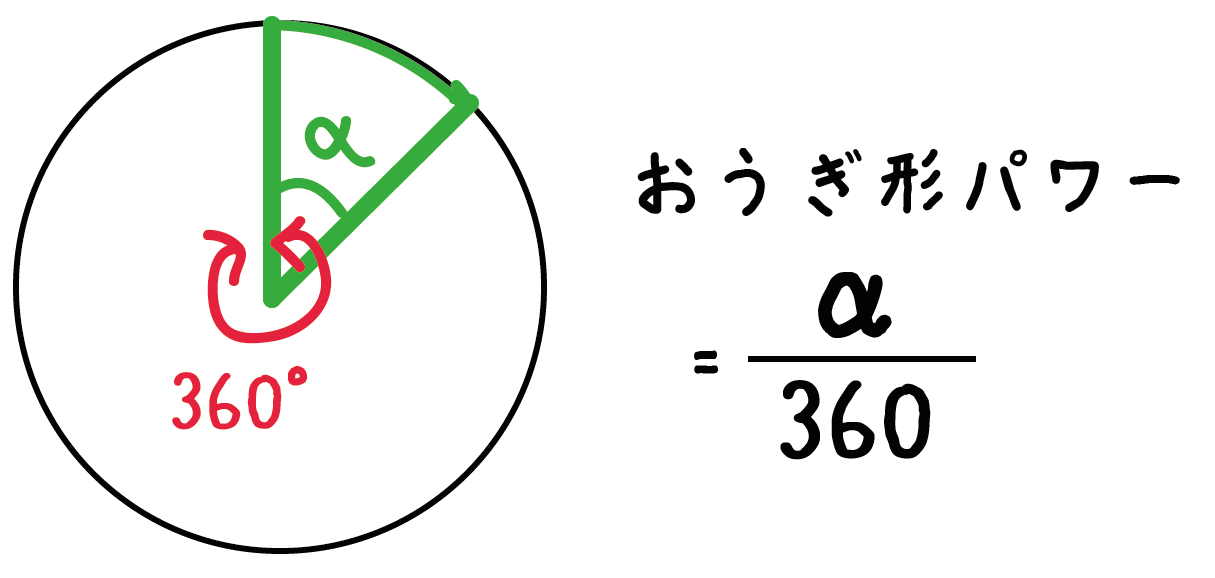



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
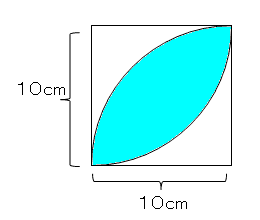



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
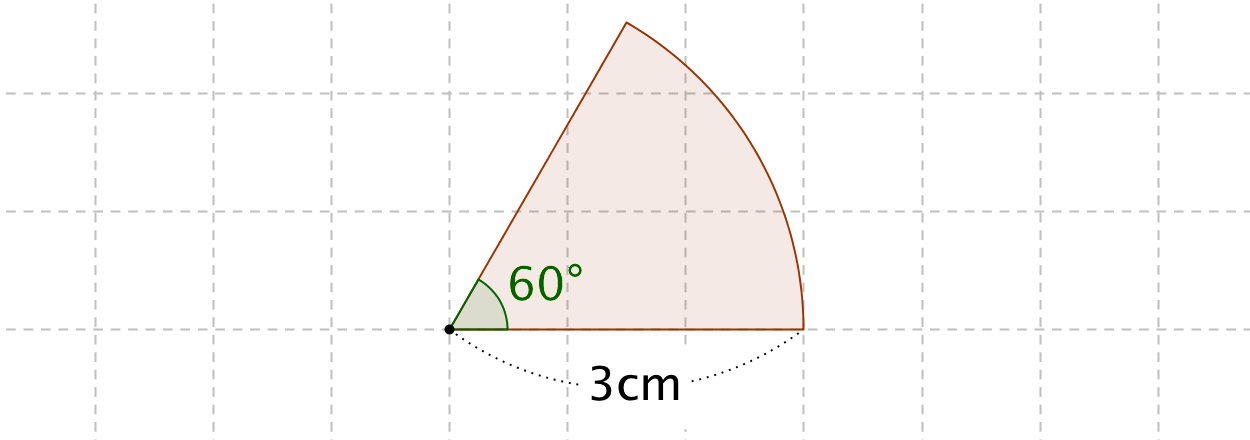



おうぎ形の面積の公式 算数の公式




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち
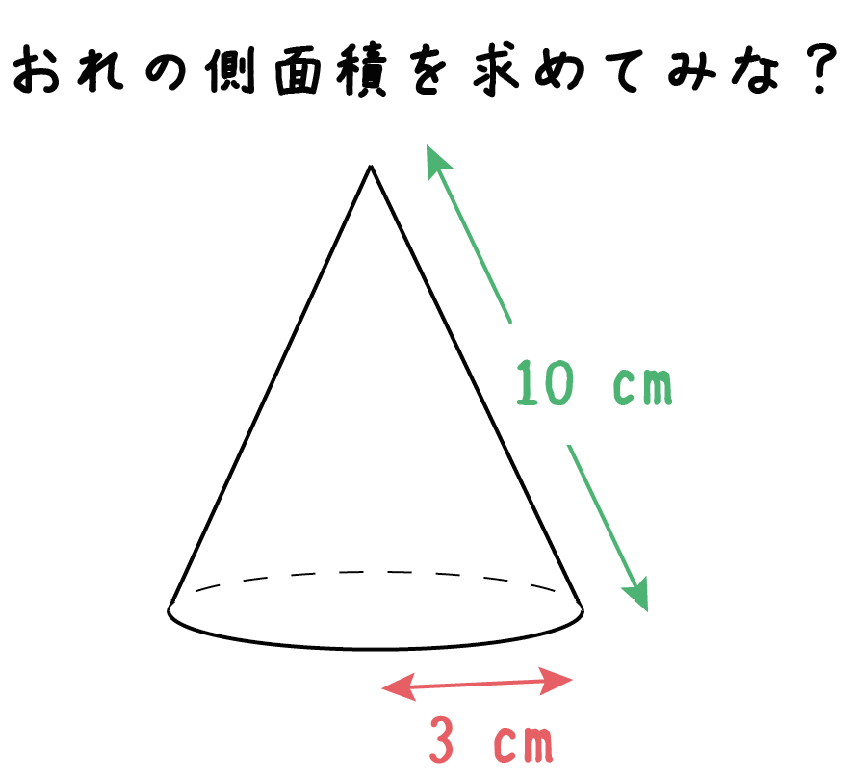



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




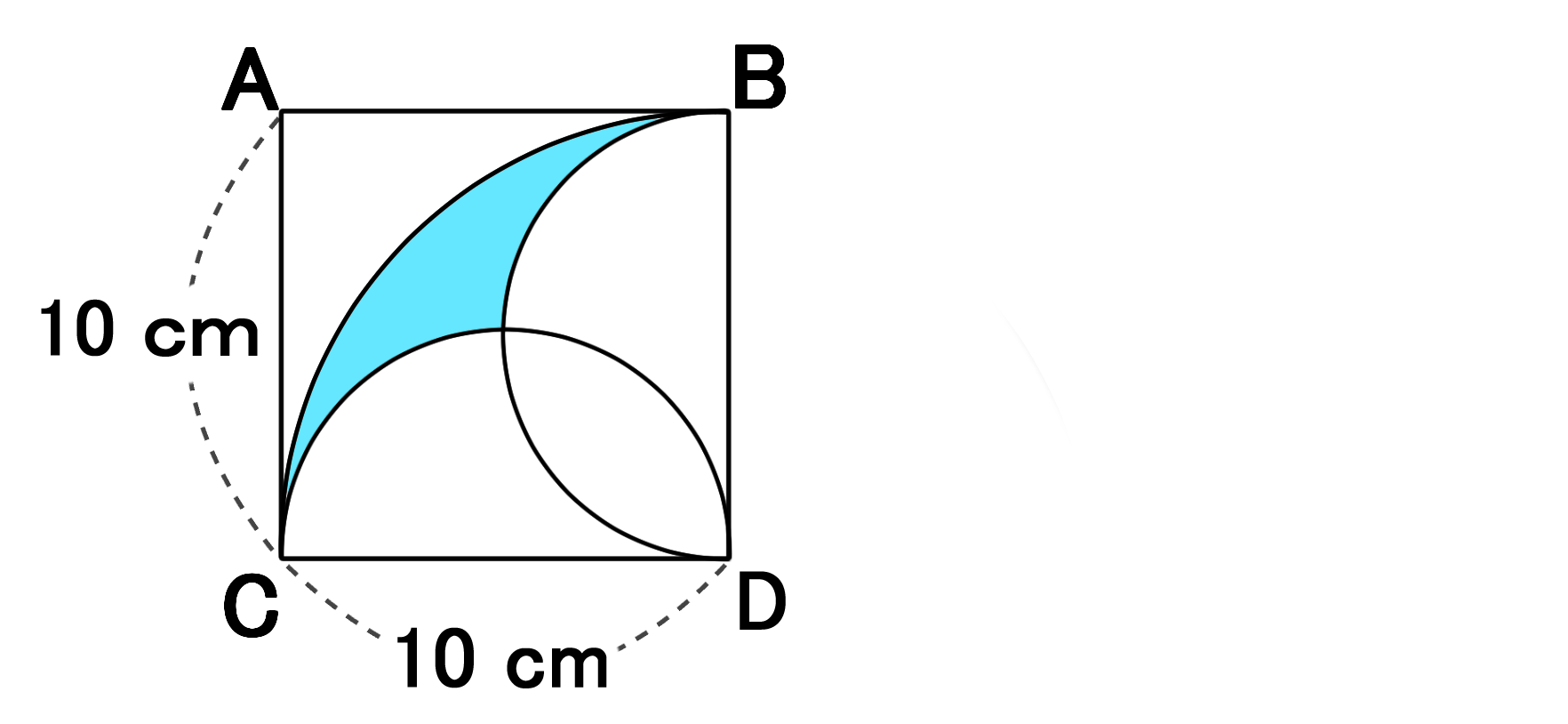
色のついた部分の面積の求め方を教えてください Clear




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




色が付いているところの面積の求め方を教えてください Clear




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月
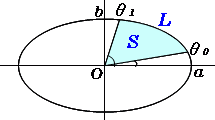



楕円扇形の面積 高精度計算サイト
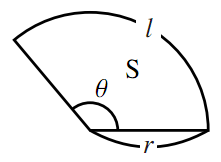



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




この扇形の面積の途中式教えてください この扇形の面積の途中式教え 中学校 教えて Goo
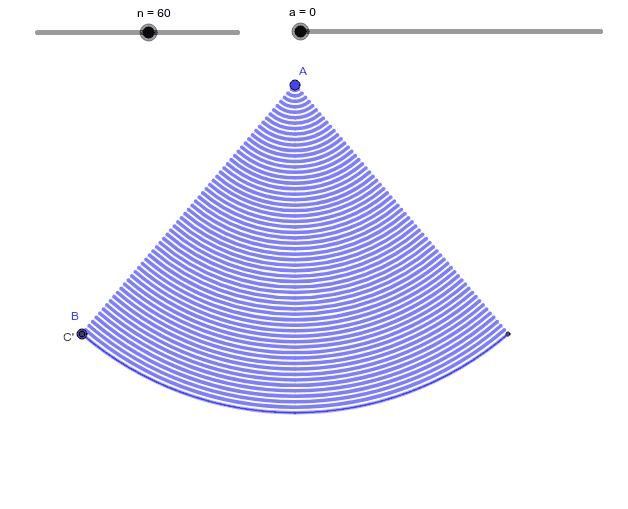



扇形の面積 Geogebra




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




極方程式の面積 扇形積分 おいしい数学




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




扇形の弧の長さと面積 計算ドリル 問題集 数学fun
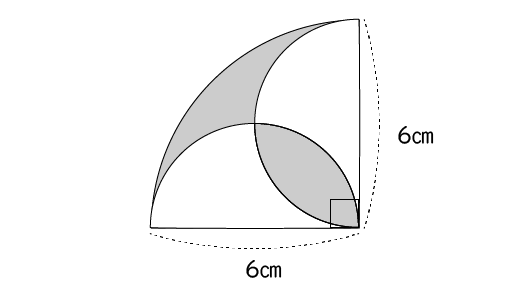



中学1年生数学 複雑な面積の求め方 長野地区 Itto個別指導学院 長野市の学習塾



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形の面積
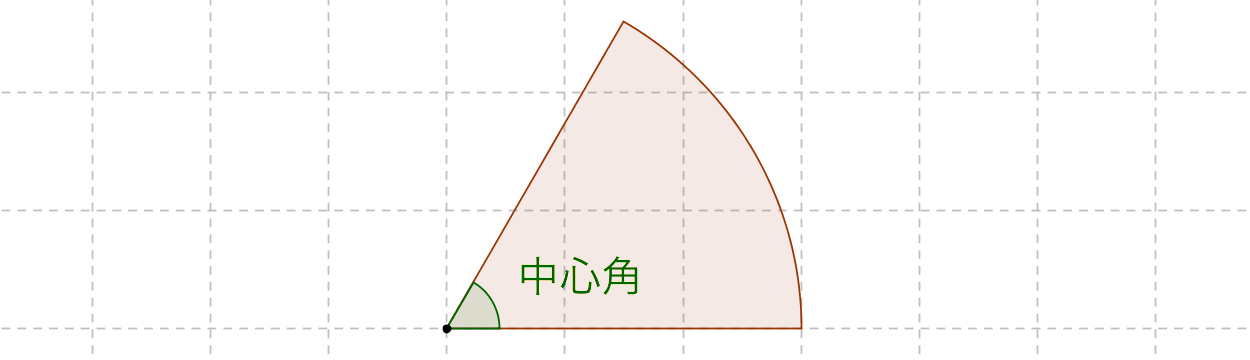



おうぎ形の面積の公式 算数の公式




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw




ボード 復習 のピン
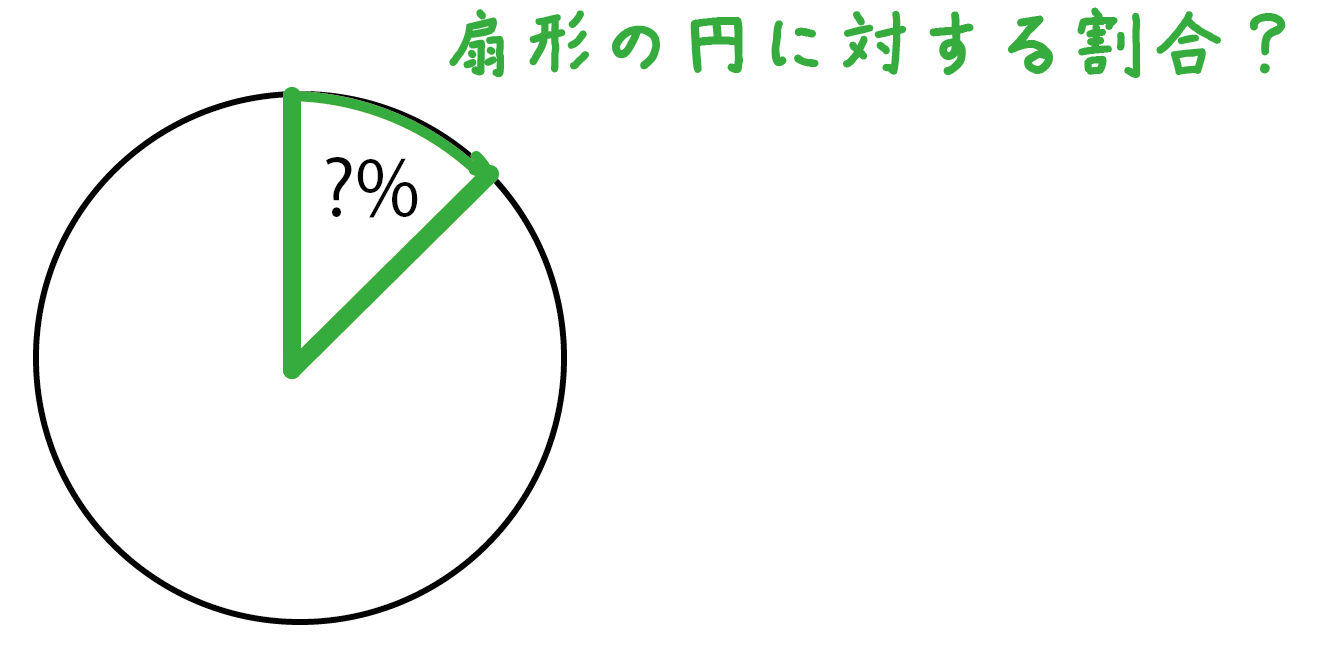



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
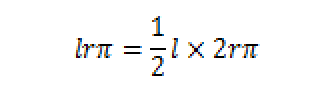



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




角錐 円錐の体積と表面積の公式 数学fun




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




扇型の求め方や中心角の求め方も分からないので 解説もお願いします この問題の答えは Clear



2



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




極方程式の面積 扇形積分 おいしい数学




円 扇形 の面積 周や弧の長さの公式 数学fun



1




半径6cm 面積10pcm の扇形の弧の長さの求め方を教えて欲しいです Clear




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張



写真の底面が扇形の立体の表面積の求め方を教えてください 特に側面積が Yahoo 知恵袋



扇形 面積の計算 計算サイト




なぜ扇形の面積にするという考えになるのですか 解説を見ても分かりませんでした Clear




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に



扇形の面積は 1分でわかる意味 公式 求め方 ラジアンとの関係




扇 おうぎ 形の面積を求める公式と弧の長さの求め方



バカでもわかる 中学数学




弧度を利用した扇の弧の長さと面積の求め方 数学ii By Okボーイ マナペディア




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



扇形の面積の求め方1 2 弧長 半径という公式が理解できません Yahoo 知恵袋
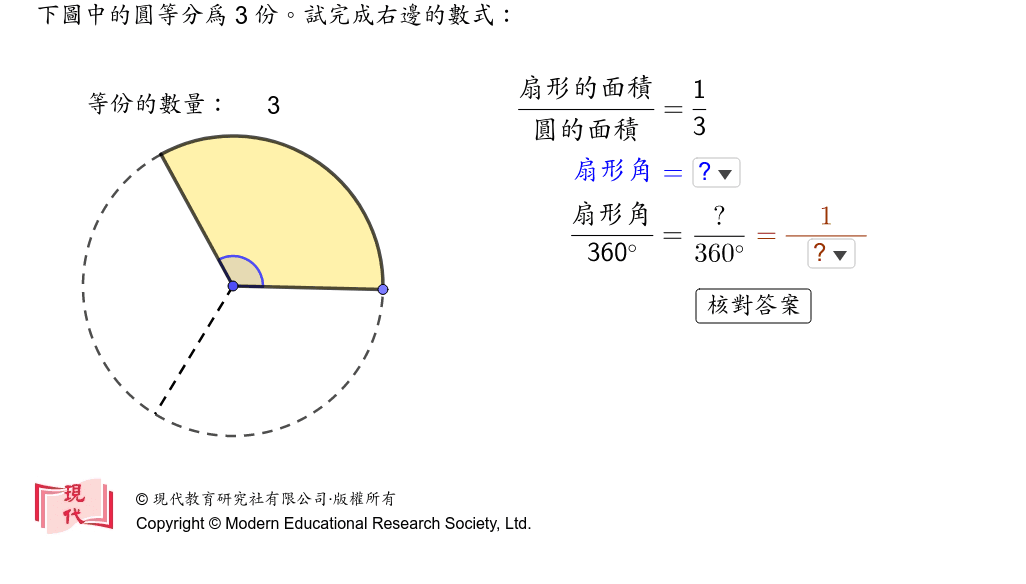



扇形面積公式 Geogebra




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



1
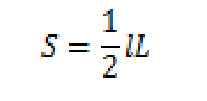



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




圓的周長與面積 19 扇形的面積計算 Youtube



7iip7agwyqgs3m



1




扇形の面積の求め方を教えてください Clear




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




円錐の表面積の求め方 You Look Too Cool




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
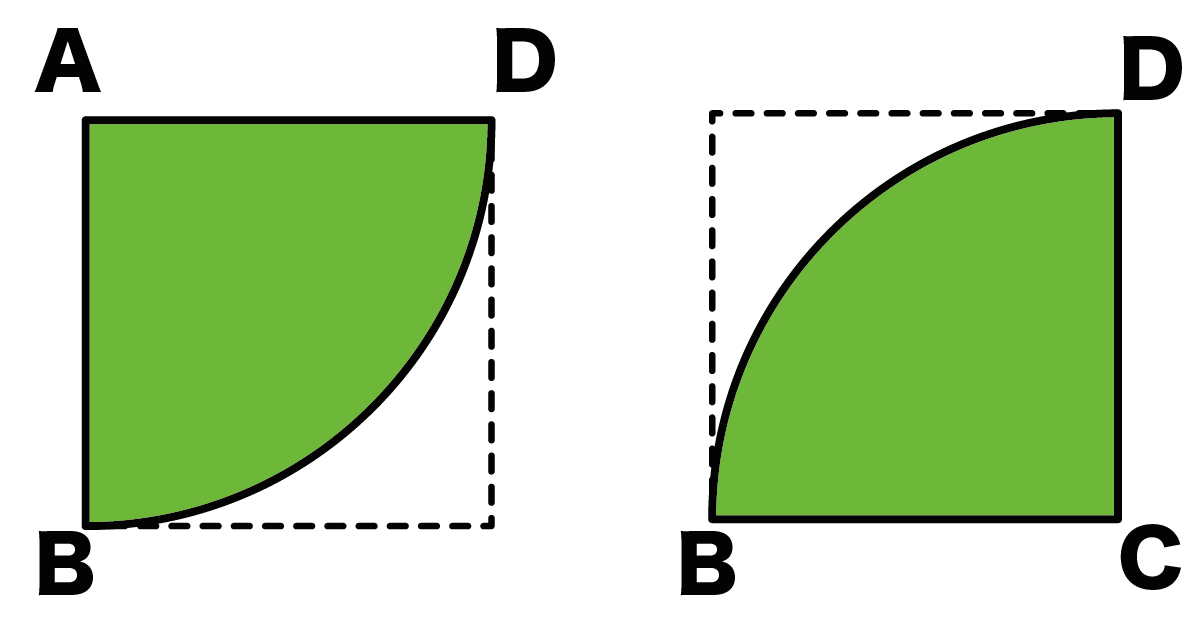



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




至急です 扇形の面積の公式を使って色がついている部分の面積を求めなさいという問題です Clear




標準 おうぎ形と正方形の面積 なかけんの数学ノート




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー
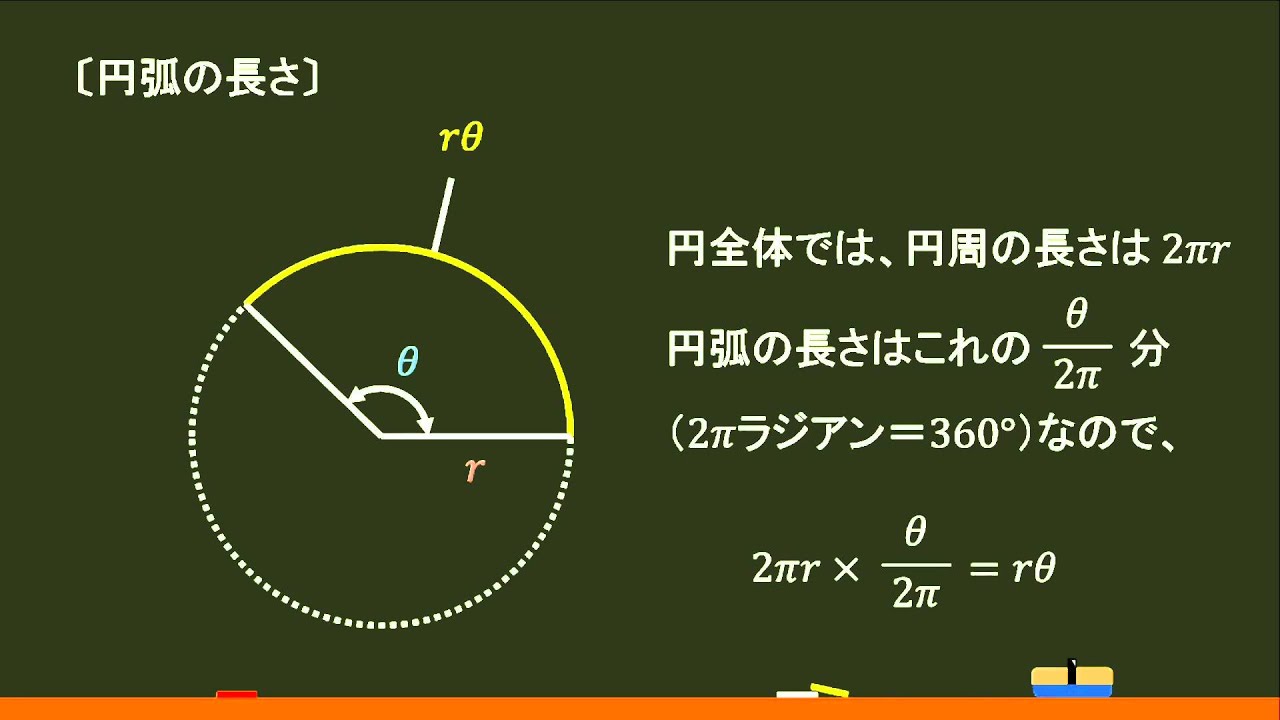



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
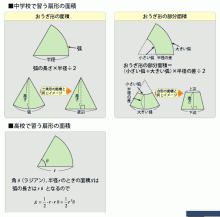



三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
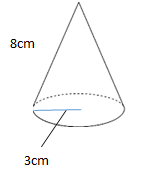



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア
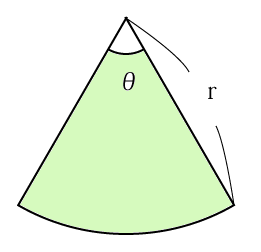



扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




扇形の弧の長さの求め方 公式と計算例


